British Flag Theorem

Dalam Geometri, British Flag Theorem menyatakan bahwa jika suatu titik $P$ adalah sembarang di dalam persegi panjang $ABCD$ maka penjumlahan kuadrat dari jarak titik $P$ ke dua sudut yang berlawanan akan sama dengan penjumlahan kuadrat dari jarak titik $P$ ke dua sudut yang berlawanan yang lain.

Teorema British Flag :
$AP^2+CP^2=BP^2+DP^2$

Bukti :
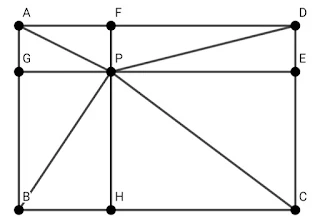
Misalkan kita tarik garis tegak lurus dari titik $P$ ke setiap sisi persegi panjang, lalu kita beri nama masing masing titik potong nya.

Maka akan berlaku teorema phytagoras pada setiap segitiga siku-siku
$AP^2=AF^2+FP^2=GP^2+FP^2$

$BP^2=BH^2+HP^2=GP^2+HP^2$
$CP^2=CH^2+HP^2=EP^2+HP^2$
$DP^2=DF^2+FP^2=EP^2+FP^2$
Perhatikan bahwa
$AP^2+CP^2=GP^2+FP^2+EP^2+HP^2$
$BP^2+DP^2=GP^2+HP^2+EP^2+FP^2$
Maka terbukti bahwa
$AP^2+CP^2=BP^2+DP^2$

Contoh Soal
Perhatikan gambar berikut

Diketahui $ABCD$ adalah persegi panjang. Jika panjang $BM=16\ \text{cm}$ dan $CM=5\ \text{cm}$, $DM=12\ \text{cm}$, maka panjang $AM$ adalah....
A. $\sqrt{15}$
B. $3\sqrt{15}$
C. $5\sqrt{15}$
D. $7\sqrt{15}$
E. $\sqrt{51}$

Jawab : Karena kita sudah tahu tentang teorema british flag, maka langsung saja kita gunakan untuk menyelesaikan soal ini yaitu
$AM^2+CM^2=BM^2+DM^2$
$AM^2+5^2=16^2+12^2$
$AM^2+5^2=20^2$ ingat pasangan phytagoras $12,16,20$
$AM^2=20^2-5^2=25.15$
$AM=5\sqrt{15}$
Maka jawaban yang tepat adalah opsi C.

Baca Juga : Segiempat Tali Busur