Teori Graf : Definisi dan Istilah Penting dalam Graf

 Pengenalan Graf

Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Sejarah graf dimulai pada saat terdapat persoalan jembatan Konigsberg (tahun 1736) yang dapat dilihat pada Gambar di bawah ini. 

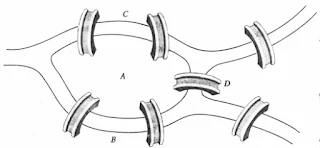Gambar 1. Jembatan Konigsberg

Terdapat tujuh jembatan pada Gambar 1, sekeras apapun seseorang mencoba tidak akan ada jalur agar seseorang bisa berjalan melintasi setiap jembatan tepat sekali. Seorang ahli matematika Swiss yaitu Leonhard Euler mempelajari fenomena ini, dan menulis sebuah artikel tentang hal tersebut. Karyanya tentang "Masalah Jembatan Konigsberg" dianggap oleh banyak orang sebagai cikal bakal dalam bidang teori graf.

Definisi Graf

Suatu Graf $G=(V,E)$ terdiri dari himpunan $V$ dan himpunan $E$, dimana $V$ adalah himpunan simpul (atau titik) tak kosong dan $E$ adalah himpunan sisi. Setiap sisi mempunyai satu atau dua simpul yang terkait dengannya, yang disebut simpul ujung. Suatu sisi dikatakan menghubungkan simpul-simpul ujungnya.

Catatan: Himpunan simpul $V$ pada $G$ memungkinkan tak hingga. Graf dengan himpunan simpul tak hingga atau jumlah sisi tak hingga dikatakan graf tak hingga. Graf dengan himpunan simpul berhingga dan himpunan sisi berhingga dikatakan graf berhingga. Graf jenis ini yang akan dibahas dalam buku ini.

Sebagai contoh, himpunan $V=\{a,b,c,d,e,f\}$, dan $E=\left\{(a,d),(a,e),(b,c),(b,e),(b,f),(c,f),(d,e),(d,f)\right\}$. Keduanya, $V$ dan $E$ merupakan graf $G$.

Kita bisa menggambarkan graf $G=(V,E)$. Pandang diagram di Gambar 2. Perhatikan bahwa setiap anggota $V$ direpresentasikan sebagai simpul atau lingkaran kecil dan setiap anggota $E$ direpresentasikan sebagai garis yang menghubungkan dua anggota $V$.

Gambar 2. Representasi Graf Secara Visual

Perhatikan bahwa setiap sisi dari graf tersebut menghubungkan dua simpul yang berbeda. Dengan kata lain, tidak ada sisi yang menghubungkan suatu simpul dengan dirinya sendiri ("loop"). Selain itu, tidak ada dua sisi berbeda yang menghubungkan pasangan simpul yang sama. Graf yang setiap sisinya menghubungkan dua simpul yang berbeda dan tidak ada dua sisi berbeda yang menghubungkan pasangan simpul yang sama disebut Graf Sederhana.

Dari strukur graf tersebut, terdapat beberapa variasi graf. Berikut ini beberapa contohnya.

1. Dengan mengganti himpunan $E$ dengan himpunan pasangan terurut di $V$, kita akan mendapatkan graf berarah atau \textit{directed graph} (digraf). Setiap sisinya memiliki arah yang spesifik.

2. Jika kita membolehkan anggota himpunan $E$ berulang, secara teknis mengganti himpunan $E$ dengan himpunan ganda, kita akan mendapatkan multigraf atau graf ganda.

3. Dengan membiarkan sisi-sisi menghubungkan suatu simpul dengan dirinya sendiri ("loop"), kita mendapatkan pseudograf atau graf semu.

4. Dengan membiarkan sisi-sisi  menjadi himpunan bagian simpul sembarang (tidak harus berpasangan), kita mendapatkan hipergraf.

5. Dengan membiarkan $V$ atau $E$ menjadi himpunan tak hingga, kita mendapatkan graf tak hingga. 

Istilah dan Konsep Dasar Graf

Pada bagian ini, akan dibahas beberapa istilah dan konsep dasar dari teori Graf. Pertama, kita diberikan istilah yang berkaitan dengan simpul dan sisi pada suatu graf tak berarah. Sebagaimana kita ketahui sebelumnya himpunan simpul pada graf $G$ dilambangkan dengan $V(G)$ atau $V$, sedangkan himpunan sisi dilambangkan dengan $E(G)$ atau $E$. Untuk memudahkan penulisan, sisi yang merepresentasikan $(u,v)$ kita tuliskan menjadi lebih sederhana menjadi $uv$. Orde graf $G$, dinotasikan sebagai $|V(G)|$ atau $|V|$, adalah kardinalitas/banyaknya anggota dari himpunan simpulnya. Ukuran graf $G$, dinotasikan sebagai $|E(G)|$ atau $|E|$, adalah kardinalitas/banyaknya anggota dari himpunan sisinya. Dua simpul $u$ dan $v$ pada graf tak berarah $G$ dikatakan bertetangga jika $u$ dan $v$ merupakan simpul ujung dari suatu sisi di $G$. Dengan kata lain $uv\in{E(G)}$. Sisi yang seperti itu disebut bersisian dengan simpul $u$ dan $v$, dan sisi terebut dikatakan menghubungkan $u$ dan $v$.

Kita juga menemukan istilah yang berguna yang menjelaskan himpunan dari simpul yang bertetangga dengan simpul tertentu pada suatu graf tak berarah.

Persekitaran (neighborhood) (atau persekitaran terbuka) dari $v$, disimbolkan dengan $N(v)$, adalah himpunan simpul-simpul yang bertetangga dengan $v$. Persekitaran tertutup dari $v$, disimbolkan dengan $N[v]$, menyatakan himpunan $\{v\}\cup N(v)$. Jika $A$ himpunan bagian dari $V$, kita notasikan $N(A)$ menyatakan himpunan semua simpul di $G$ yang bertetangga dengan setidaknya satu simpul di $A$. Jadi, $N(A)=\cup_{v\in A}N(v)$. Serupa bahwa $N[A]=A\cup N(A)$.

Untuk mengetahui berapa banyak sisi yang bersisian pada suatu simpul kita juga dikenalkan dengan istilah berikut. Derajat dari suatu simpul di graf tak berarah adalah banyaknya sisi yang bersisian dengan simpul tersebut, kecuali bahwa loop pada suatu simpul menyumbang dua kali derajat dari simpul tersebut. Derajat dari suatu simpul $v$ dilambangkan dengan $\deg(v)$.

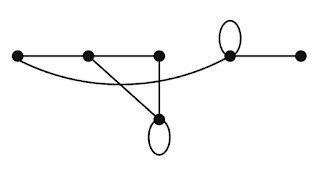
Contoh : Hitunglah derajat dan apa saja persekitaran dari simpul-simpul pada graf $G$ dan $H$ berikut.

Jawab: Pada graf $G$, $\deg(a)=2$, $\deg(b)=\deg(c)=\deg(f)=4$, $\deg(d)=1$, $\deg(e)=3$, dan $\deg(g)=0$. Persekitaran simpul-simpulnya adalah $N(a)=\{b,f\}$, $N(b)=\{a,c,e,f\}$, $N(c)=\{b,d,e,f\}$, $N(d)=\{c\}$, $N(e)=\{b,c,f\}$, $N(f)=\{a,b,c,e\}$, dan $N(g)=\emptyset$. Sedangkan pada graf $H$, $\deg(a)=4$, $\deg(b)=\deg(e)=6$, $\deg(c)=1$, dan $\deg(d)=5$. Persekitaran simpul-simpulnya adalah $N(a)=\{b,d,e\}$, $N(b)=\{a,b,c,d,e\}$, $N(c)=\{b\}$, $N(d)=\{a,b,e\}$, dan $N(e)=\{a,b,d\}$.

Simpul yang berderajat nol disebut simpul terpencil (isolated). Oleh sebab itu suatu simpul terpencil tidak bertetangga dengan simpul manapun. Simpul $g$ pada graf $G$ di Contoh di atas merupakan simpul terpencil. Suatu simpul merupakan \textbf{simpul anting (\textit{pendant})} jika dan hanya jika simpul tersebut memiliki derajat satu. Akibatnya, simpul anting bertetangga dengan tepat satu simpul lain. 

Simpul $d$ pada graf $G$ di Contoh 1 merupakan simpul anting.

Contoh :

Kemudian tentukan simpul mana sajakah pada graf tersebut yang termasuk simpul terpencil dan yang termasuk simpul.anting.

Jawab: Sisi-sisi pada graf tersebut merepresentasikan persaingan antara simpul-simpul yang bersisian dengannya. Pada graf tersebut, derajat yang mewakili tupai adalah $4$, karena tupai bersaing dengan empat spesies lainnya: gagak, opposum, rakun, dan pelatuk. derajat yang mewakili tupai adalah $4$. Dalam graf tersebut, tikus adalah satu-satunya spesies yang diwakili oleh simpul anting, karena tikus hanya bersaing dengan tikus tanah dan semua spesies lain bersaing dengan setidaknya dua spesies lain. Tidak ada simpul terpencil dalam graf tersebut karena setiap spesies dalam ekosistem ini bersaing dengan setidaknya satu spesies lain.

Derajat maksimum suatu graf $G$, dilambangkan dengan $\Delta(G)$ didefinisikan sebagai $\Delta(G)=\text{max}\left\{\deg(v)\, |\, v\in V(G)\right\}$

Derajat minimum suatu graf $G$, dilambangkan dengan $\delta(G)$ didefinisikan sebagai

$\delta(G)=\text{min}\left\{\deg(v)\, |\, v\in V(G)\right\}$

Barisan derajat suatu graf berorde $n$ adalah barisan $n$ suku (biasanya ditulis dengan barisan menurun) dari derajat-derajat simpulnya.

Contoh 3 : Pandang graf pada Gambar 2. Pada graf tersebut, mempunyai orde $6$ dan ukuran $8$; simpul $a$ dan $d$ bertetangga sedangkan simpul $a$ dan $b$ tidak bertetangga; $N(d)=\{a,e,f\}$, $N[d]=\{a,d,e,f\}$; $\Delta(G)=3$, $\delta(G)=2$; dan barisan derajat adalah $3,3,3,3,2,2$.